Velocity table

Problem:



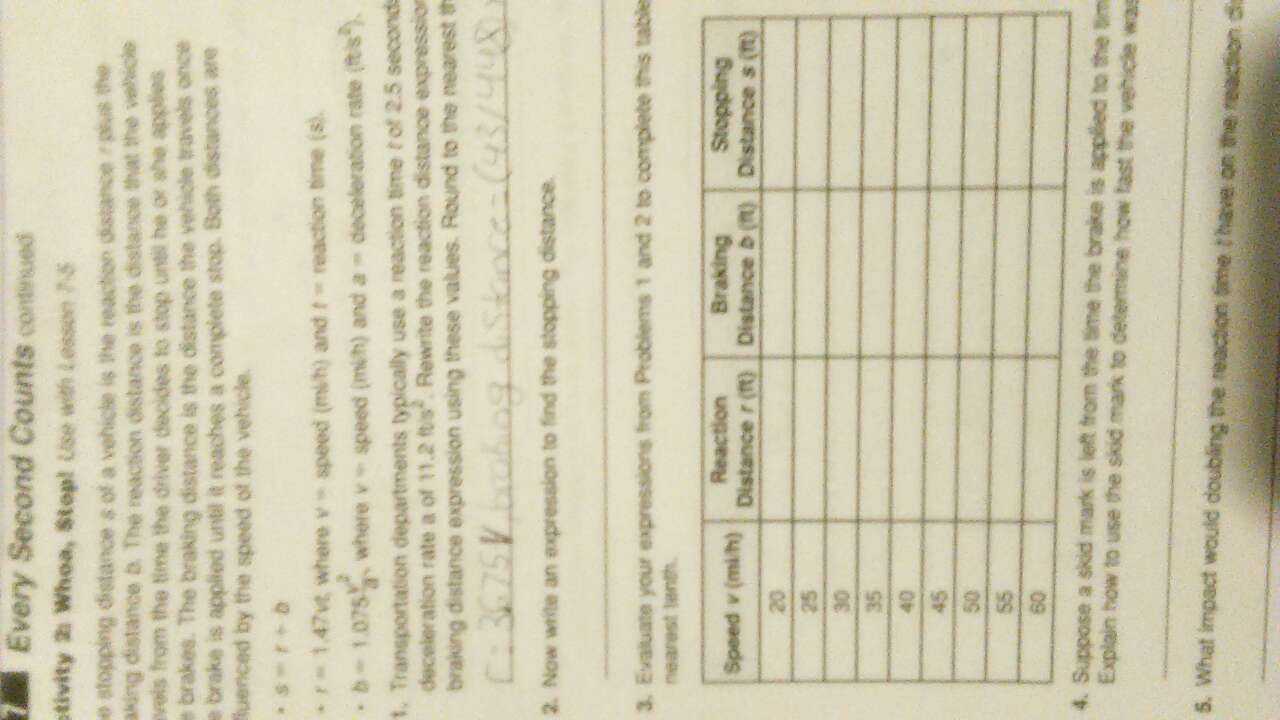
Solution:

The reaction distance is $ r = 3.675v $
The braking distance is $ b = \frac{43}{448}v^2 $
The stopping distance is $ s = 3.675v + \frac{43}{448}v^2 $

The table is

v	reaction	braking	stopping
20	73.5	38.39286	111.8929
25	91.875	59.98884	151.8638
30	110.25	86.38393	196.6339
35	128.625	117.5781	246.2031
40	147	153.5714	300.5714
45	165.375	194.3638	359.7388
50	183.75	239.9554	423.7054
55	202.125	290.346	492.471
60	220.5	345.5357	566.0357

We can solve for $ v $ by using the skid mark. The length of the skid mark is the same as stopping distance.

If we double the reaction time, the reaction distance would double.