Some physics problems (1)

Problem:

Two blocks A and B are adjacent to each other on a smooth surface, case 1 block A pushes block B as shown. In case 2 block B pushes block A as seen above. The Force F is 3,0 N in both examples.  a) Calculate the acceleration of the blocks in case 1. b) Does the blocks get the same acceleration in case 2? Explain your answer.  c) Calculate the forces acting between the block A and B in both cases.



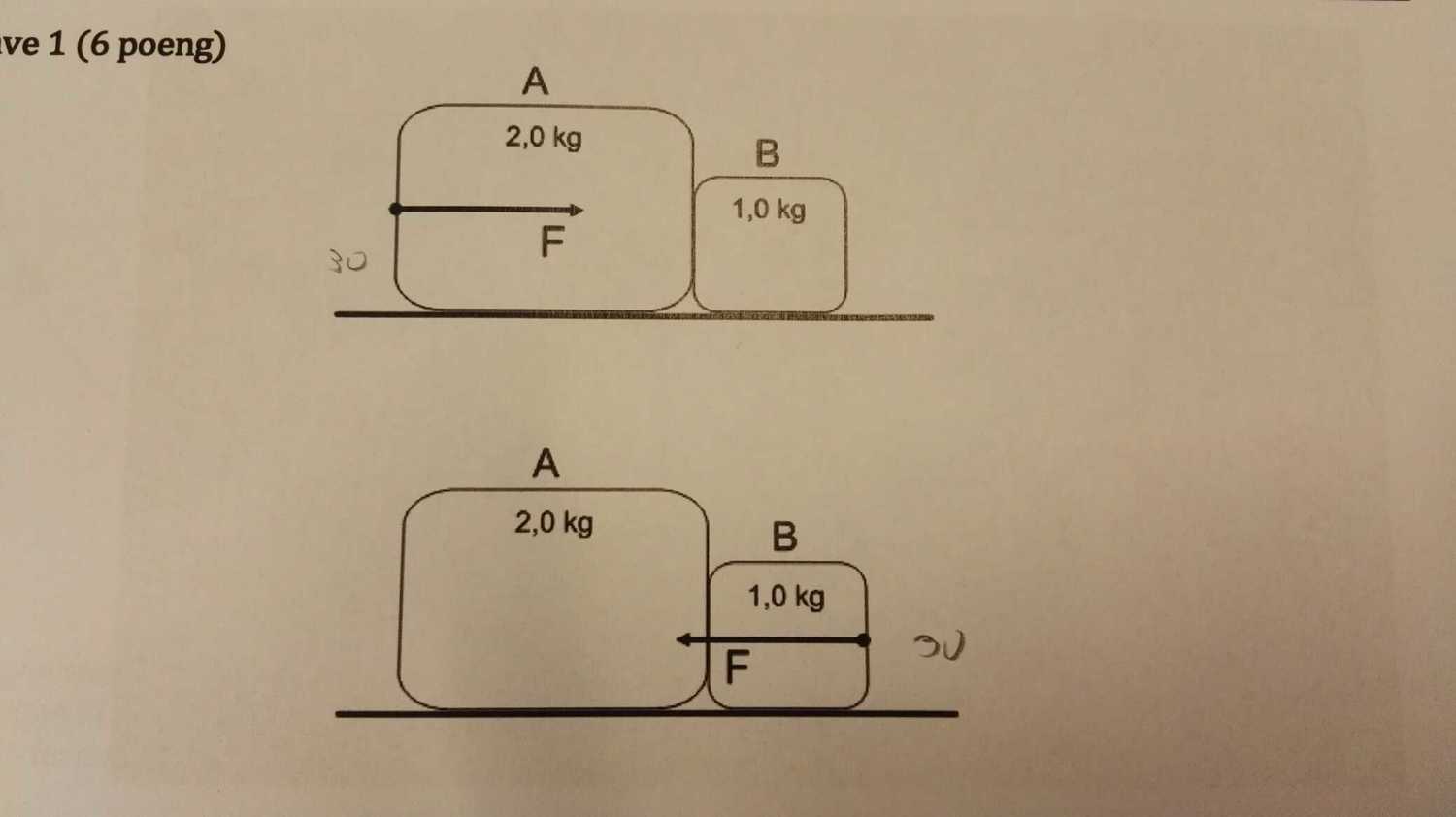
Solution:

I guess you mean 3.0 N

Part a) To calculate the acceleration, we use Newton's second law on the overall object (i.e. A and B together considered 1 object)

$ \begin{eqnarray*} F &=& ma \\ 3.0 &=& (2.0 + 1.0)a \\ a &=& 1 kg m s^{-2} \\ \end{eqnarray*} $

Part b) Yes, they are the same, we simply considered the two blocks as a single object in the last question, so it does not matter which side do we push.

Part c) in this case we use the free body diagram technique.

For case 1, there is only one force exerted on B, that would be the contact force $ F_{AB} $ exerted by A to B, so we use the Newton's second law again

$ \begin{eqnarray*} F &=& ma \\ F_{AB} &=& 1.0 (1) \\ &=& 1 N \\ \end{eqnarray*} $

Block A is conceptually harder, apparently we applied a force 3N to it, the block A exert 1N contact force to block B, so by Newton's third law block B also exert a 1N reaction force to it. The net force exerted on block A is the 3N from left to right and 1N from right to left, so we have 2N from left to right. That also explain the acceleration when Newton's second law when applied to A alone.
Therefore overall there are 3 forces:

1. $ F_{AB} $ contact force applied by A to B = 1N
2. $ F_{BA} $ reaction force of the above by B to A = 1N
3. $ F_{HA} $ human pushed A = 3N

The case 2 is exactly the same and here is a list of forces for that case

1. $ F_{AB} $ contact force applied by B to A = 2N
2. $ F_{BA} $ reaction force of the above by A to B = 2N
3. $ F_{HB} $ human pushed B = 3N