Some physics problem (5)

Problem:

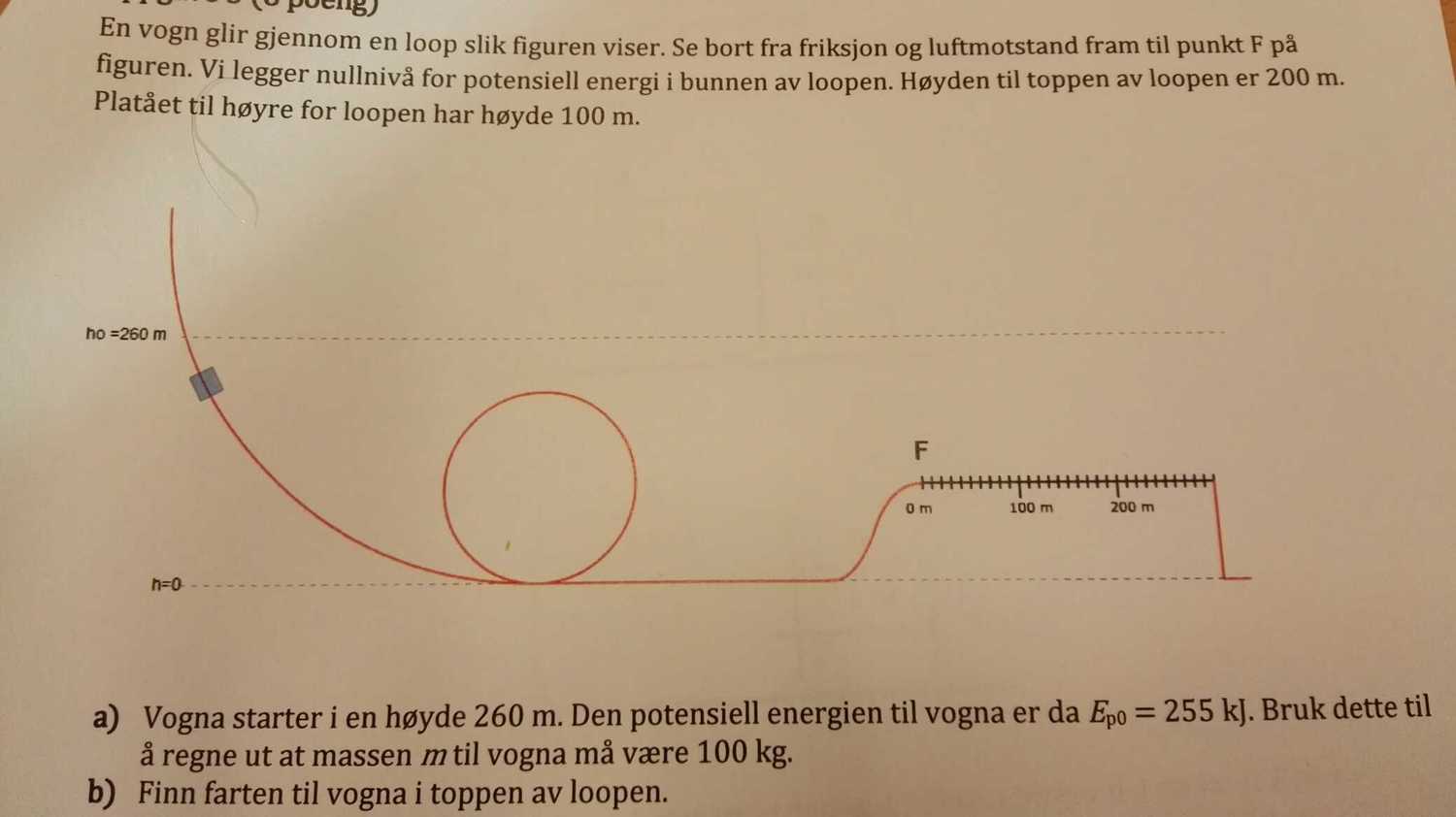
A) the wagon starts at an altitude 260 m. The potential energy of the wagon is then 255 kj .Use this to calculate the mass m to the wagon must be 100 kg

b Find the speed of the wagon in the top of the loop.

On the plateau, point F on the figure, it puts friction on the wagon. The carriage stops after it has moved after the stretch s = 229 m after point F.

C) How big is the friction number between the plateau and the cart?



Solution:

Part a)

$255KJ = 255 \times 1000 J$ = Potential energy = $mgh = m(9.8)(260)$.

Therefore $m = 100.08 kg$.

Part b)

When the wagon start, it has 0 kinetic energy (it hasn't started yet, no velocity there) and 255kj potential energy.

At the top of the loop, it has potential energy $mgh = 100 \times 9.8 \times 200 = 196000 J = 196KJ$, the rest must be accounted for as kinetic energy due to energy conservation.

The kinetic energy is then $255 - 196 = 59KJ = 59000 J = \frac{1}{2}mv^2 = 50v^2$. Therefore the velocity is $34.35... ms^{-1}$.

Part C) Using energy conservation we similarly compute the velocity at the beginning of the track to be $56.03... ms^{-1}$.

According to the Coulomb friction model, the friction is constant along the slide, which means we will have a constant deceleration. The v-t graph of the wagon should look like this, and at this point we do NOT know the x-intercept

The area under curve is the distance travelled, and that we know it is 229m, therefore, the x-intercept is calculated by solving the triangle area.

$\frac{1}{2}56.03 \times t = 229$, so we solve $t = 8.17...s$.

With that, we know the deceleration has to be $\frac{56.03}{8.17} = 6.86... kgms^{-2}$

Finally, $F = ma$ give us the friction as $100 \times 6.86... = 685.59 N$.