Roots

Problem:

Question 1

Solution:

a) $ 2\sqrt{14} + 5\sqrt{14} = 7\sqrt{14} $
b) $ 5\sqrt{17} -0.8\sqrt{17} = 4.2\sqrt{17} $
c) $ 12\sqrt{6} - 5\sqrt{6} - 7\sqrt{6} = -\sqrt{6} $
d) $4.5\sqrt{3} - 0.7\sqrt{3} = 3.8 \sqrt{3} $
e) $\frac{8}{11}\sqrt{17} - \frac{5}{11}\sqrt{17} = \frac{3}{11}\sqrt{17} $
f) $1.5\sqrt{13} - 1.7\sqrt{13} - 4\sqrt{13} = -4.2\sqrt{13} $

Exponents

Problem:



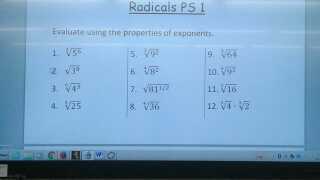
Solution:

The general method of solving these problems is

Step 1) Write the root as a fraction power.

For example, $ \sqrt[3]{5^6} = (5^6)^{\frac{1}{3}} $
$ \sqrt{3^6} = (3^6)^{\frac{1}{2}} $

Step 2) Multiply the exponents

For example, $ (5^6)^{\frac{1}{3}} = 5^{6 \times \frac{1}{3}} = 5^2 $
$ (3^6)^{\frac{1}{2}} = 3^{6 \times \frac{1}{2}}= 3^3 $.

That's it.

Calculus

Problem:

Solution:

Implicitly differentiate both side, we have

$ \frac{d(\cot{2x} - 2\csc{xy})}{dx} = \frac{dy^2}{dx} $
$ -2\csc{2x} + 2\csc(xy)\cot(xy)(y + x\frac{dy}{dx})= 2y\frac{dy}{dx} $
$ -2\csc{2x} + 2y\csc(xy)\cot(xy)= (2y - 2x\csc(xy)\cot(xy))\frac{dy}{dx} $
$ \frac{dy}{dx} = \frac{2y\csc(xy)\cot(xy) - 2\csc{2x}}{2y - 2x\csc(xy)\cot(xy)} $

The next problem is simply repeated application of the chain rule:

$ \frac{dy}{dx} = 3(3e^{4x} + 4x^2\ln(x))\frac{d(3e^{4x} + 4x^2\ln(x))}{dx} $
$ \frac{dy}{dx} = 3(3e^{4x} + 4x^2\ln(x))(12e^{4x} + \frac{d(4x^2\ln(x))}{dx}) $
$ \frac{dy}{dx} = 3(3e^{4x} + 4x^2\ln(x))(12e^{4x} + 4x^2\frac{1}{x} + 8x\ln(x)) $
$ \frac{dy}{dx} = 3(3e^{4x} + 4x^2\ln(x))(12e^{4x} + 4x + 8x\ln(x)) $

The last problem is trivial, just plot it.

Limit

Problem:

Solution:

$ \lim\limits_{x \to \infty}{\frac{\sqrt{4x + 4x^2}}{4x + 5}} $
= $ \lim\limits_{x \to \infty}{\frac{\frac{\sqrt{4x + 4x^2}}{x}}{\frac{4x + 5}{x}}} $
= $ \lim\limits_{x \to \infty}{\frac{\sqrt{\frac{4x + 4x^2}{x^2}}}{\frac{4x + 5}{x}}} $
= $ \lim\limits_{x \to \infty}{\frac{\sqrt{\frac{4}{x} + 4}}{4 + \frac{5}{x}}} $
= $ \frac{\sqrt{4}}{4} $
= $ \frac{1}{2} $

Derivative

Problem:



Solution:

Part a)

Part b)

Part c)

Part d)

Math

Problem:



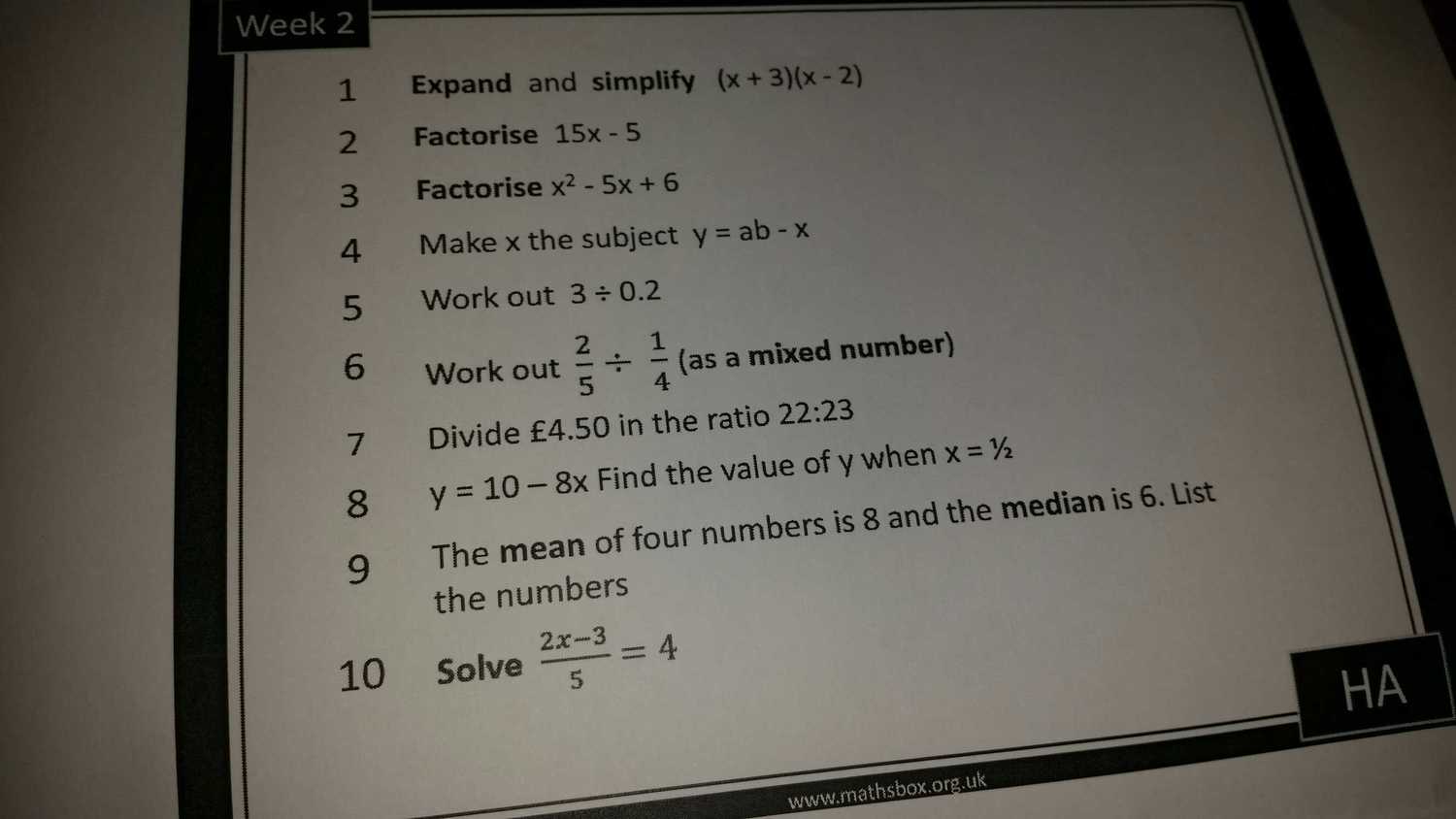
(6 - 10) with working

Solution:

6) $ \frac{2}{5} \div \frac{1}{4} = \frac{2}{5} \times \frac{4}{1} = \frac{8}{5} = 1\frac{3}{5} $.

7)
$ 4.5 \times \frac{22}{22 + 23} =  4.5 \times \frac{22}{45} = 2.2 $
$ 4.5 \times \frac{23}{22 + 23} =  4.5 \times \frac{23}{45} = 2.3 $

8) $ y = 10 - 8x = 10 - 8 \times \frac{1}{2} = 10 - 4 = 6 $
9) The easiest way is to assume the middle two numbers are 6, now the sum of the two them is 12, the sum of the rest must be $ 8 \times 4 - 12 = 32 - 12 = 20 $, we can satisfy it with 1, 19.

So the four numbers are 1, 6, 6, 19.

10) $ x = \frac{4 \times 5 + 3}{2} = \frac{23}{2} = 11\frac{1}{2} $

Some more chemistry problems

Problem:



Solution:

1)
Electronegativity increase from left to right in the periodic table because of octet rule.
Electronegativity decreease from top to bottom in periodic table because of atomic size.

a) Silicon < Sulfur < Chlorine [rule 1 above]
b) Rubidium < Potassium < Sodium [rule 2 above]

2)
a) Ionic: Rb+ Cl-
b) Covalent: S = S
c) Polar Covalent N $ \equiv $ P (electron will be more close to N than P)
d) Covalent $ CF_4 $

3)
Atomic radius increase from right to left (they share similar orbitals in the same row, but with increased number of protons the orbital size decreases)
Atomic radius increase from top to bottom due to adding more orbitals.

a)  $ O^{2-} < S^{2-} < SE^{2-} < TE^{2-} $, this is rule 2

They are isoelectronic with Ne, Ar, Kr, Xe respectively

b) $ I < Te < Ba < Cs $, this is rule 1 and rule 2 combined.

They are isoelectronic with Xe, Xe, Rn, Rn respectively.

4) We need to break 2 H-S bond, 3 F-F bond, that requires energy
$ 347  \times 2 + 154 \times 3 = 1156 KJ $.

Then we form 4 S-F bonds, 2 HF bonds, that give out energy
$ 4 \times 327 + 2 \times 565 = 2438 KJ $.

Therefore the reaction is $\delta H = 1238 - 2438 = -1282 KJ $

Long division

Problem:



Solution:

Boolean logic

Problem:



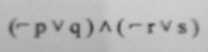
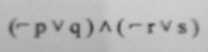
Solution:

P	Q	R	S	(NOT(P) OR Q) AND (NOT(R) OR S)
FALSE	FALSE	FALSE	FALSE	TRUE
FALSE	FALSE	FALSE	TRUE	TRUE
FALSE	FALSE	TRUE	FALSE	FALSE
FALSE	FALSE	TRUE	TRUE	TRUE
FALSE	TRUE	FALSE	FALSE	TRUE
FALSE	TRUE	FALSE	TRUE	TRUE
FALSE	TRUE	TRUE	FALSE	FALSE
FALSE	TRUE	TRUE	TRUE	TRUE
TRUE	FALSE	FALSE	FALSE	FALSE
TRUE	FALSE	FALSE	TRUE	FALSE
TRUE	FALSE	TRUE	FALSE	FALSE
TRUE	FALSE	TRUE	TRUE	FALSE
TRUE	TRUE	FALSE	FALSE	TRUE
TRUE	TRUE	FALSE	TRUE	TRUE
TRUE	TRUE	TRUE	FALSE	FALSE
TRUE	TRUE	TRUE	TRUE	TRUE

Some physics problems (4)

Problem:

Kevin Bania has created chaos online with his new video on youtube. From standing position, he jumps 162.5 centimeters above the ground.

Physics Professor Rhett Alain user Banias record jumps to say something about gravity (weight point is the same as the point of attack for gravity) and how it affects resilience. Allain provides an estimate of where the gravity to Bania is located (stomach area) and calculates how high of a record the man actually jumped. The answer is 86 cm, the rest of the 162,5 cm retrieves Bania gets when he pulls his legs up under himself

a) Add the zeropoint for potential energy in Banias gravity and assume Bania has a mass of 75 kg. Show that the rise in potential energy is 0, 63 KJ

b) From the video it takes ca.1.2 seconds to do the jump. What is the theoretical minimum worth we may have for effect at a displacement on 86 cm?

c) will the answer in b) be a realistic measurement for a real jump? Discuss simplifications and idealizations that underlie the calculation.

Solution:

Part a)

The potential energy change is $ mgh = 75 \times 9.8 \times 0.86 = 632.1 J = 0.63 KJ $.

Part b)

With some clarification, we actually wanted the minimum force to achieve the height.

To calculate that, we have a sketch of the v-t  graph as such

At this point, we do not know the actual y-values, the x-values are accurate. At the initial point we have an sudden change in velocity still to the jump, once he leave the ground however, he cannot exert any force and then driven by gravity. The drop part is similar, he receive a collision impact with the ground, and eventually stop.

The area of the left triangle should be the height he jumped, so we have $ \frac{1}{2} v_{max} \times 0.6 = 0.86 $, solving get $ v_{max}= 2.87... ms^{-1} $.

Assuming it take 0.01s second to leave the ground (the usual impact time), the acceleration is $ \frac{2.87}{0.01} = 286.67 $, the force is $ 75 \times 286.67 = 21,500 N $.

Part c)

No, the value above simply does not make sense at all. A few thousand Newton's is what an extreme person can deliver. 21,500N is simply mission impossible.

Some physics problem (5)

Problem:

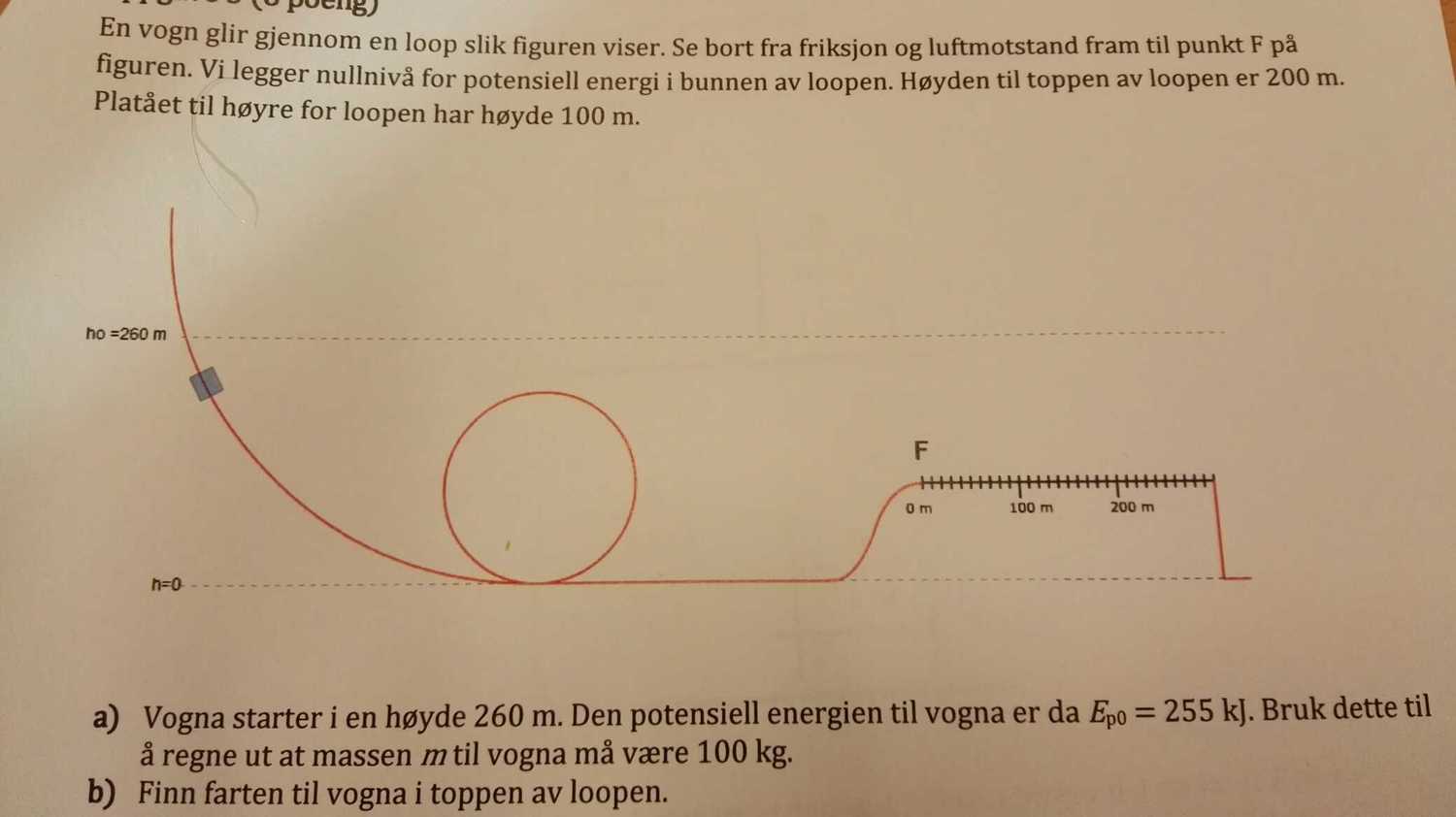
A) the wagon starts at an altitude 260 m. The potential energy of the wagon is then 255 kj .Use this to calculate the mass m to the wagon must be 100 kg

b Find the speed of the wagon in the top of the loop.

On the plateau, point F on the figure, it puts friction on the wagon. The carriage stops after it has moved after the stretch s = 229 m after point F.

C) How big is the friction number between the plateau and the cart?



Solution:

Part a)

$ 255KJ = 255 \times 1000 J $ = Potential energy = $ mgh = m(9.8)(260) $.

Therefore $ m = 100.08 kg $.

Part b)

When the wagon start, it has 0 kinetic energy (it hasn't started yet, no velocity there) and 255kj potential energy.

At the top of the loop, it has potential energy $ mgh = 100 \times 9.8 \times 200 = 196000 J = 196KJ $, the rest must be accounted for as kinetic energy due to energy conservation.

The kinetic energy is then $ 255 - 196 = 59KJ = 59000 J = \frac{1}{2}mv^2 = 50v^2 $. Therefore the velocity is $ 34.35... ms^{-1} $.

Part C) Using energy conservation we similarly compute the velocity at the beginning of the track to be $ 56.03... ms^{-1} $.

According to the Coulomb friction model, the friction is constant along the slide, which means we will have a constant deceleration. The v-t graph of the wagon should look like this, and at this point we do NOT know the x-intercept

The area under curve is the distance travelled, and that we know it is 229m, therefore, the x-intercept is calculated by solving the triangle area.

$ \frac{1}{2}56.03 \times t = 229 $, so we solve $ t = 8.17...s $.

With that, we know the deceleration has to be $ \frac{56.03}{8.17} = 6.86... kgms^{-2} $

Finally, $ F = ma $ give us the friction as $ 100 \times 6.86... = 685.59 N $.

Some physics problems (3)

Problem:

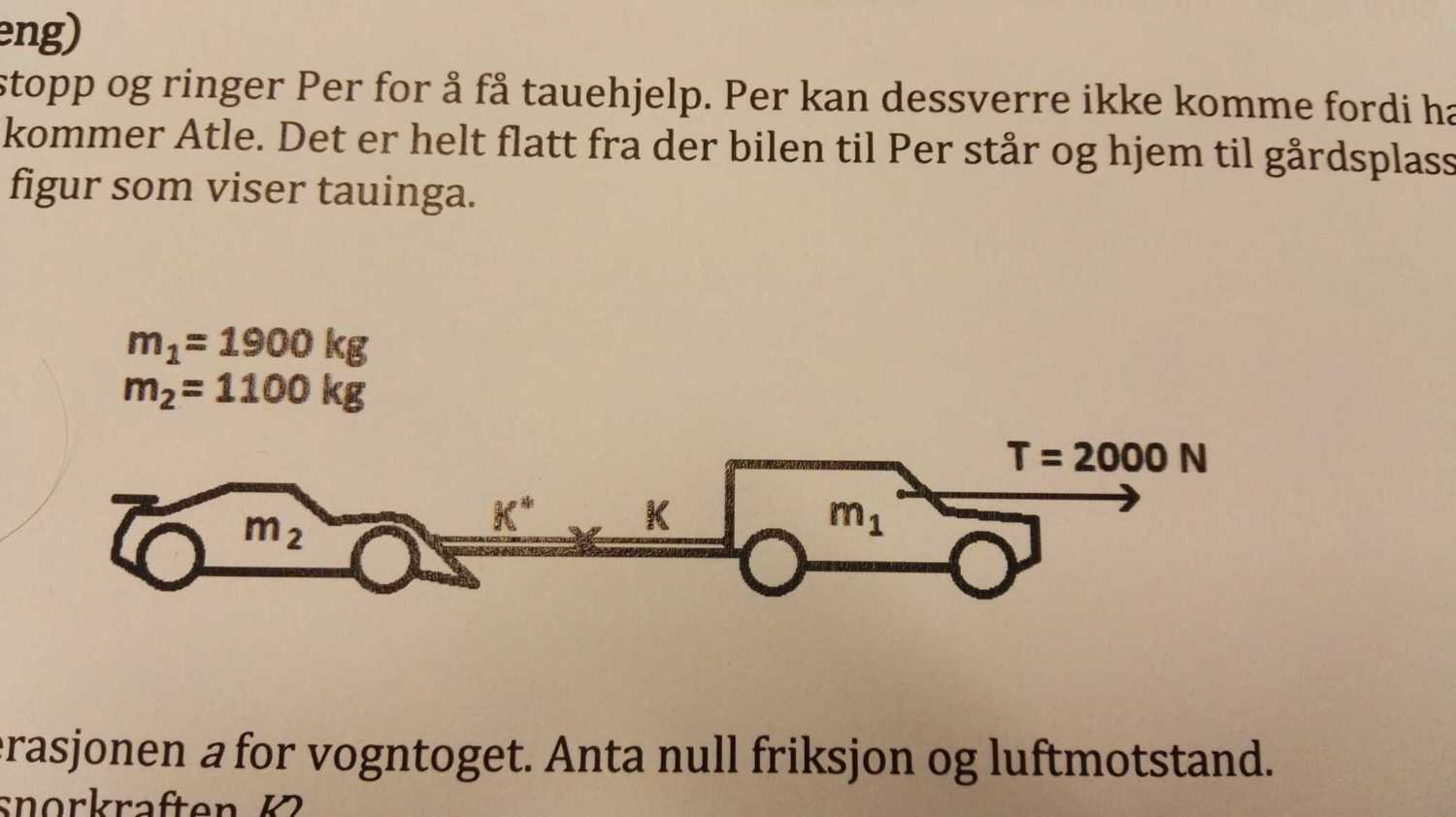
Jack has got an engine failure and is calling Janice to get towing assistance. Janice unable to come because he is in the middle of dinner. Instead, Atle comes. It is completely flat from where the car to Per stands and home to the courtyard. Below is a figure showing the towing.

a) Calculate the acceleration of a wagon train. Assume zero friction and air resistance.

b) What will the string power K become?



Solution:

By applying Newton's second law to the whole object,we have

$ \begin{eqnarray*} F &=& ma \\ 2000 &=& (1900+1100)a \\ a &=& \frac{2}{3} kgms^{-2} \\ \end{eqnarray*} $

Part b)

There is no such thing called string power. I guess the problem is asking for the tension developed on the string.

Once again, we apply the Newton's second law, but this time to $ m_2 $.


$ \begin{eqnarray*} F &=& ma \\ K &=& (1100)\frac{2}{3} \\ &=& \frac{2200}{3} N \\ \end{eqnarray*} $

By Newton's third law, the same tension is applied from the string to both cars.

Roots

Problem:



Solution:

You can write it these two ways

$ (\sqrt[5]{26})^2 $ or $ \sqrt[5]{26^2} $, both mean exactly the same expression.

Simple random sampling

Problem:



Solution:

A good question to ask!

To do a simple random sampling, you need to make sure you know the martial and health status of all parents (so that you do not randomly sampled a person who is not accessible). With the population perfectly known, you generate sample without replacement in the population and do the study with that sample.

To do convenience sampling, you simply wait outside the door at the school. By the time parent comes pick up the student, you just ask. See how much simpler this is than the approach above? The approach, however, is not as good as simple random sampling as one might expect. You may miss all busy parents who do not pick up their children punctually.

To do voluntary response sample. You simply ask every student to take home a questionnaire. Parent may voluntary give answers, that is voluntary response sampling technique. This is also simple, again, bias towards parents who are more free and willing to do questionnaire.

Some physics problem (2)

Problem:

Few materials have as great value as gold. You have inherited an old gold jewelry, but will pledge it to get money for a new car. Using Arkhimedes' law you find that jewelry has a volume corresponding to 7.10-^5 m^3 Gold has a price per kilo of NOK. 207 000, -. How much money can you get for the jewelry ?

Solution:

The price can be found by volume x density x unit price.

The volume is given, the price is given, the problem is the density.

So I looked up the density in Wikipedia as follow:

https://en.wikipedia.org/wiki/Gold

Density near r.t.	19.30 g/cm3

To solve the puzzle, we need to also convert the units.

$ 1kg/m^3 = 1000g / m^3 = 1000g /(100 cm)^3 = 1000g/1000000cm^3 = 1g/1000cm^3 $.

Therefore, $ 1 g/cm^3  = 1000kg/m^3 $

Now we have all the pieces, the answer is

$ 7 \times 10^{-5} \times 19.30 \times 1000 \times 207000 = 279657 NOK $

By the way, NOK is not a valid currency code?

Some physics problems (1)

Problem:

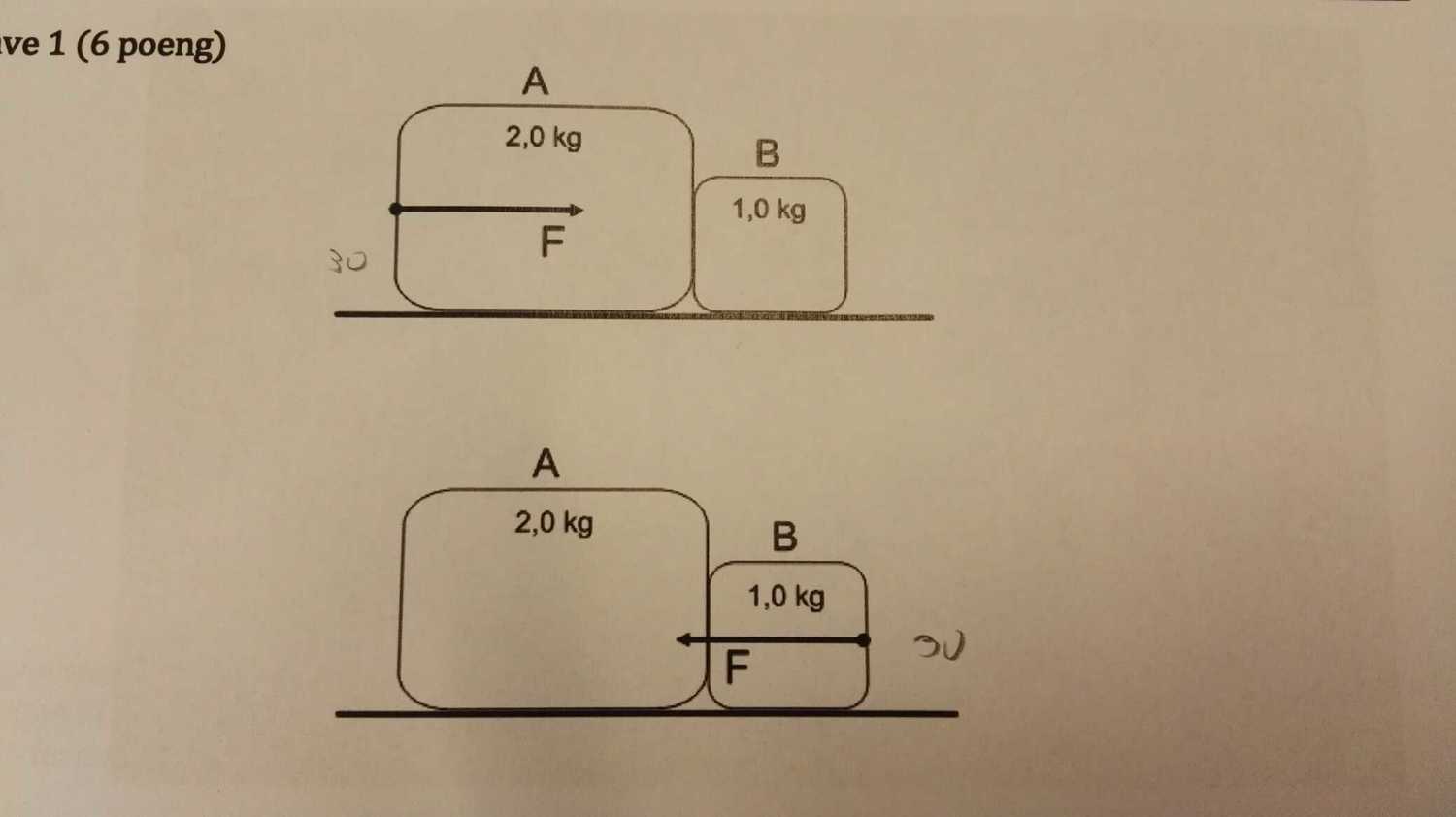
Two blocks A and B are adjacent to each other on a smooth surface, case 1 block A pushes block B as shown. In case 2 block B pushes block A as seen above. The Force F is 3,0 N in both examples.  a) Calculate the acceleration of the blocks in case 1. b) Does the blocks get the same acceleration in case 2? Explain your answer.  c) Calculate the forces acting between the block A and B in both cases.



Solution:

I guess you mean 3.0 N

Part a) To calculate the acceleration, we use Newton's second law on the overall object (i.e. A and B together considered 1 object)

$ \begin{eqnarray*} F &=& ma \\ 3.0 &=& (2.0 + 1.0)a \\ a &=& 1 kg m s^{-2} \\ \end{eqnarray*} $

Part b) Yes, they are the same, we simply considered the two blocks as a single object in the last question, so it does not matter which side do we push.

Part c) in this case we use the free body diagram technique.

For case 1, there is only one force exerted on B, that would be the contact force $ F_{AB} $ exerted by A to B, so we use the Newton's second law again

$ \begin{eqnarray*} F &=& ma \\ F_{AB} &=& 1.0 (1) \\ &=& 1 N \\ \end{eqnarray*} $

Block A is conceptually harder, apparently we applied a force 3N to it, the block A exert 1N contact force to block B, so by Newton's third law block B also exert a 1N reaction force to it. The net force exerted on block A is the 3N from left to right and 1N from right to left, so we have 2N from left to right. That also explain the acceleration when Newton's second law when applied to A alone.
Therefore overall there are 3 forces:

1. $ F_{AB} $ contact force applied by A to B = 1N
2. $ F_{BA} $ reaction force of the above by B to A = 1N
3. $ F_{HA} $ human pushed A = 3N

The case 2 is exactly the same and here is a list of forces for that case

1. $ F_{AB} $ contact force applied by B to A = 2N
2. $ F_{BA} $ reaction force of the above by A to B = 2N
3. $ F_{HB} $ human pushed B = 3N

Math questions (2)

Problems:



Solutions:

6a) $ a = 15000(1 + \frac{0.0475}{365})^{365t} $
6b) 19020.83103
6c) 6.05685876

7a) $ p = 50000e^{0.055t) $
7b) Approximately 233229.5135
7c) 7.372092875 years since 1980
7d)

UDAB has population more than FILO at between 11th and 12th year since 1980.

Math questions

Problems:



Solutions:

8a) y intercept = 0
8b) x intecepts = 0, -2
8c) The vertical asymptotes are
x = -1
x = -2
8d) The horizontal asymptote is
y = 1

8e) The graph look like this, the jump parts actually goes to infinity ...

 

9a)

9b) 80 feets

9c) 96 feets

9d)  between 3.4 seconds and 3.5 seconds

Some Statistics (3)

Problem:

 

Solution:

The population is the 750 students.
The sample is the 100 students randomly selected.

Some Statistics (2)

Problem:



Solution:

Very often, census is mission impossible - suppose we want to know the average age of a man, if we do census right now, we have to wait until they all die to know how long they actually lived! Isn't that rather useless?

Even in case where census is possible, it might give low return on high cost. If we knew the distribution, we already know how much error we are going to have in the sample statistics (such as the sample mean), and if the error is within a reasonable bound for the problem at hand, then it is good enough. Again, take the life span as an example, if we knew the life span distribution is normal, and we have already sampled a lot of human life span data, then there is no point getting even more, because we know the error is going to be small, we don't need to know whether the actual average life span is 77.124 or 77.123, we just don't care.

Some statistics (1)

Problem:



Solution:

Who will win the next U.S. presidential election?

Population: All voters in US
Sample: Some voters in US that one can pick.

Is my well water safe?

Population: Everyone that can access the well.
Sample: The owner of the well, or maybe his families.

Are as many girls born as boys in the world?

Population: Everyone on the planet.
Sample: Some people on the planet one can pick.

Which work better, Advil or Tylenol?

Population: We need to be more specific with the question - presumably the question is asking which of the two drugs are better in treating cold, if so, the population is the set of all patients with cold.
Sample: Some set of people having cold have cold.

Do student who take more math classes in high school get into better colleges?

Population: All high school students
Sample: Some high school students.

More Chemistry Problems

Problem:



Solution:

Question 6

	Full	Abbreviated	Valence
Silicon	$1s^2 2s^2 2p^6 $	[Ne] $ 3s^2 3p^2 $	4
Calcium	$ 1s^2 2s^2 2p^6 3s^2 3p^2 4s^2 $	[Ar] $ 4s^2 $	2
Manganese	$ 1s^2 2s^2 2p^6 3s^2 3p^2 4s^2 3d^5 $	[Ar] $4s^2 3d^5 $	7
Bromine	$ 1s^2 2s^2 2p^6 3s^2 3p^2 4s^2 3d^{10} 4p^5 $	[Ar] $ 4s^2 3d^{10} 4p^5 $	7
Krypton	$ 1s^2 2s^2 2p^6 3s^2 3p^2 4s^2 3d^{10} 4p^{6} $	[Kr]	8

Question 7

	+ electron affinity	+ Ionization energy	+ size
Carbon and Nitrogen	Nitrogen	Nitrogen	Carbon
Argon and Bromine	Argon	Argon	Bromine
Magnesium and Potassium	Magnesium	Magnesium	Potassium
Fluorine and Chlorine	Florine	Florine	Chlorine

Question 8

$ Li_3N $
$ NaBr $
$ K_2S $

Transformer

Problem:



Solution:

To reflect over the x-axis, you set the new x coordinate to be the old x coordinate and the new y coordinate to be the negative of the old y coordinate.

Therefore the reflected coordinates are

(2, 2)
(2, -3)
(-4, 2)

To rotate 90 degree clockwise about the origin, you set new x coordinate to be the old y coordinate and the new y coordinate to be the negative of the old x coordinate

Therefore the rotated coordinates are

(2, -2)
(-3, -2)
(2, 4)

Finally, to translate three unit down and 2 unit left, you set the new x coordinate to be the old x-coordinate - 2 and the new y coordinate to be the old y-coordinate - 3.

Therefore the translated coordinates are

(0, -5)
(-5, -5)
(0, 1)

Statistical modeling

Problem:



Solution:

First, let make a raw plot

It looks like power law, let's take a look at the log-log plot

So it make sense, as weight should proportional to volume proportional to length cube. Let's do a cubic model

Notice I purposefully set the y-intercept of the regression line to be 0.

Another parabola

Problem:



Solution:

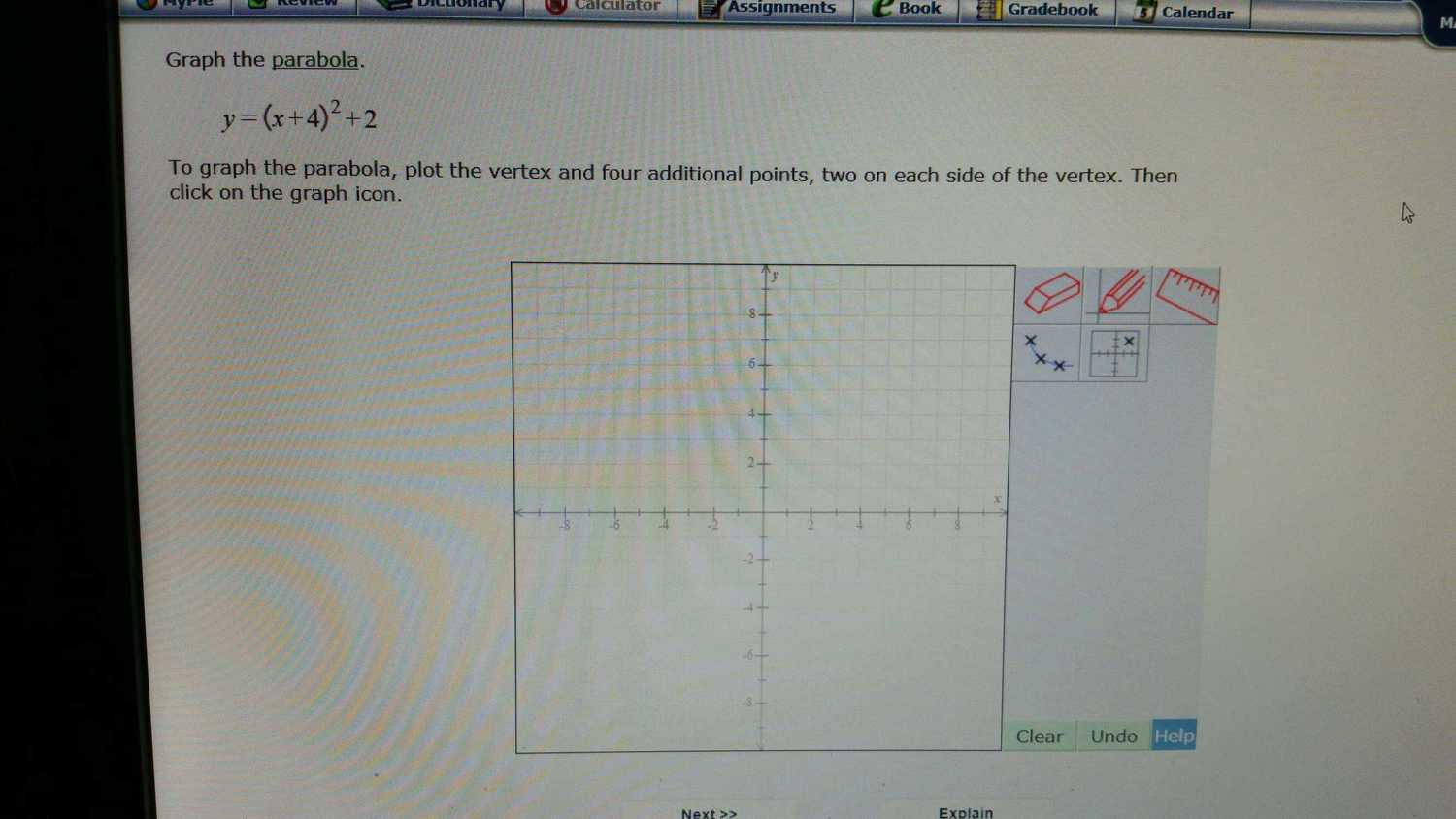
These are the point I used to plot the parabola.

(-6, 6)
(-5, 3)
(-4, 2)
(-3, 3)
(-2, 6)

And here is the plot:

Plot yet another parabola

Problem:



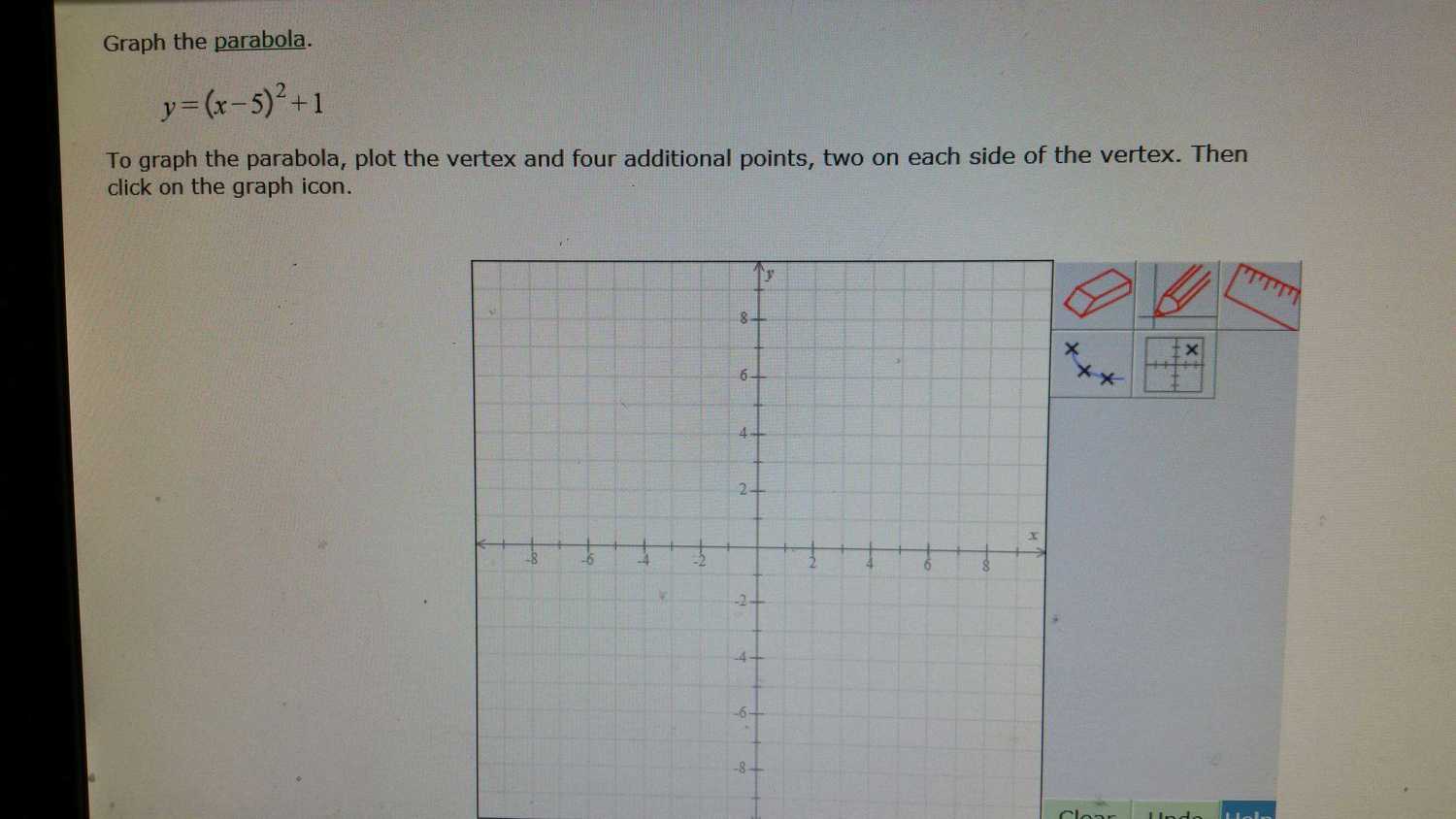
Solution:

These are the point I used to plot the parabola.

(3, 5)
(4, 2)
(5, 1)
(6, 2)
(7, 5)

And here is the plot:

Mechanics

Problems:



Solution:

1.) It is traveling towards South.

2.1) It accelerated towards North from 0 minutes to 10 minutes
2.2) It maintained constant speed towards North from 10 minutes to 15 minutes.
2.3) It decelerates and eventually stop from 15 minutes to 30 minutes.
2.4) It accelerated towards South from 30 minutes to 40 minutes.
2.5) It decelerated towards South eventually stop from 40 minutes to 55 minutes.

3.) 300 meters

4.) 1,050 meters

5.) -4 meter per second squared

6.) 500 meters

7.) 1,550 meters

8.) 550 meters

Plot another parabola

Problem:



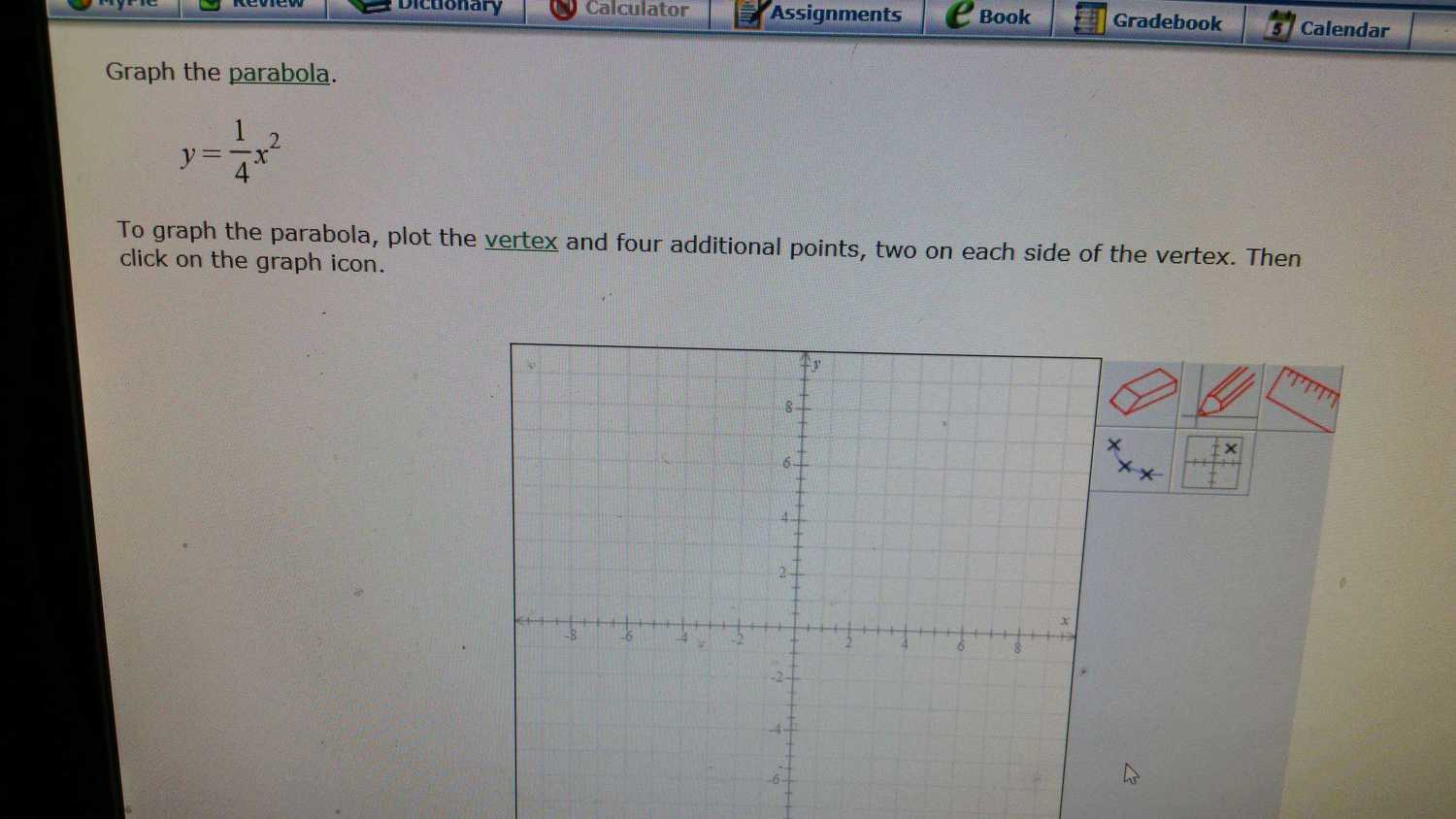
Solution:

These are the point I used to plot the parabola.

(-2, 1)
(-1, 0.25)
(0, 0)
(1, 0.25)
(2, 1)

And here is the plot:

Plot parabola

Problem:



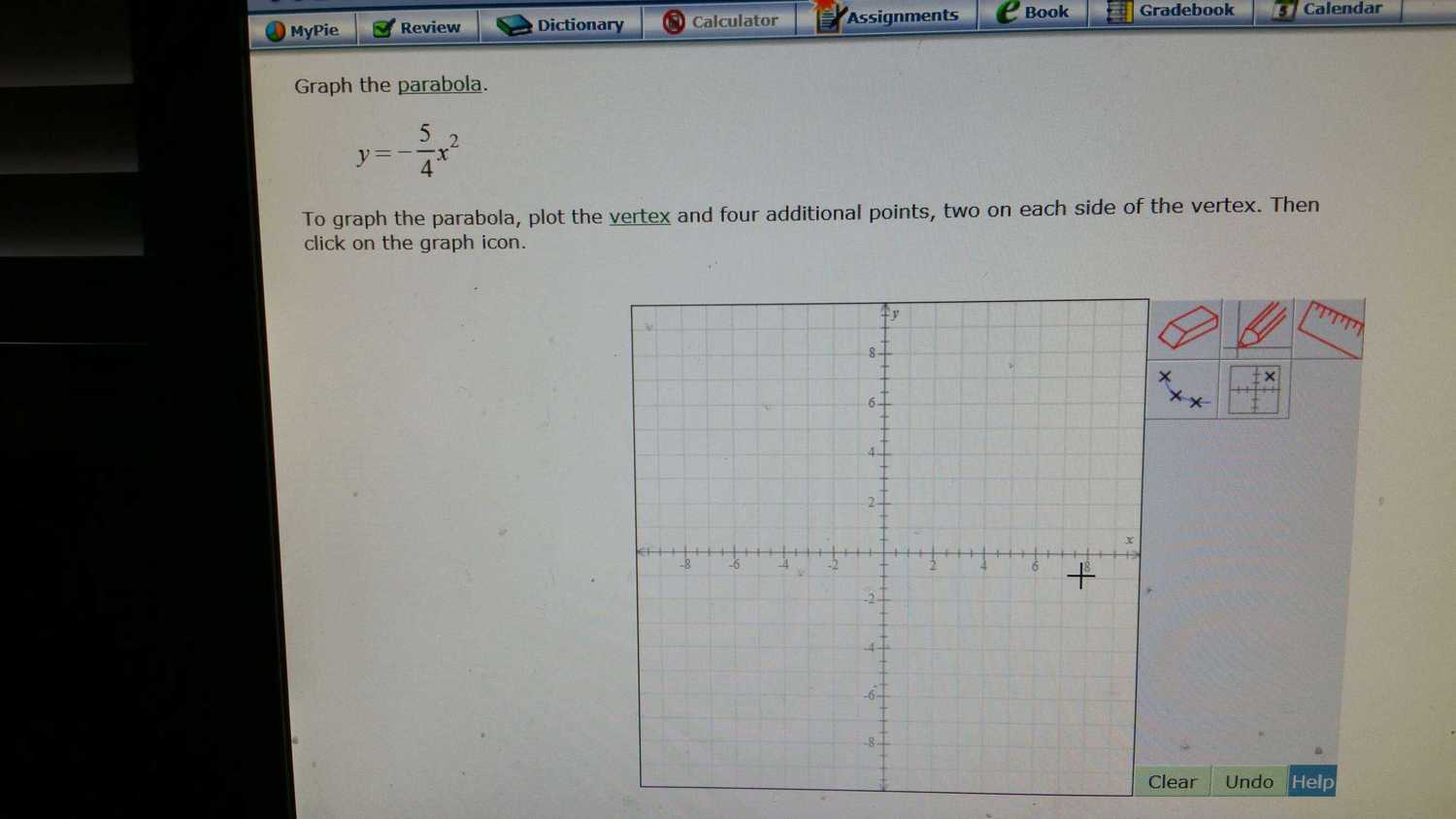
Solution:

These are the point I used to plot the parabola.

(-2, -5)
(-1, -1.25)
(0, 0)
(1, -1.25)
(2, -5)

And here is the plot:

Measure

Problem:



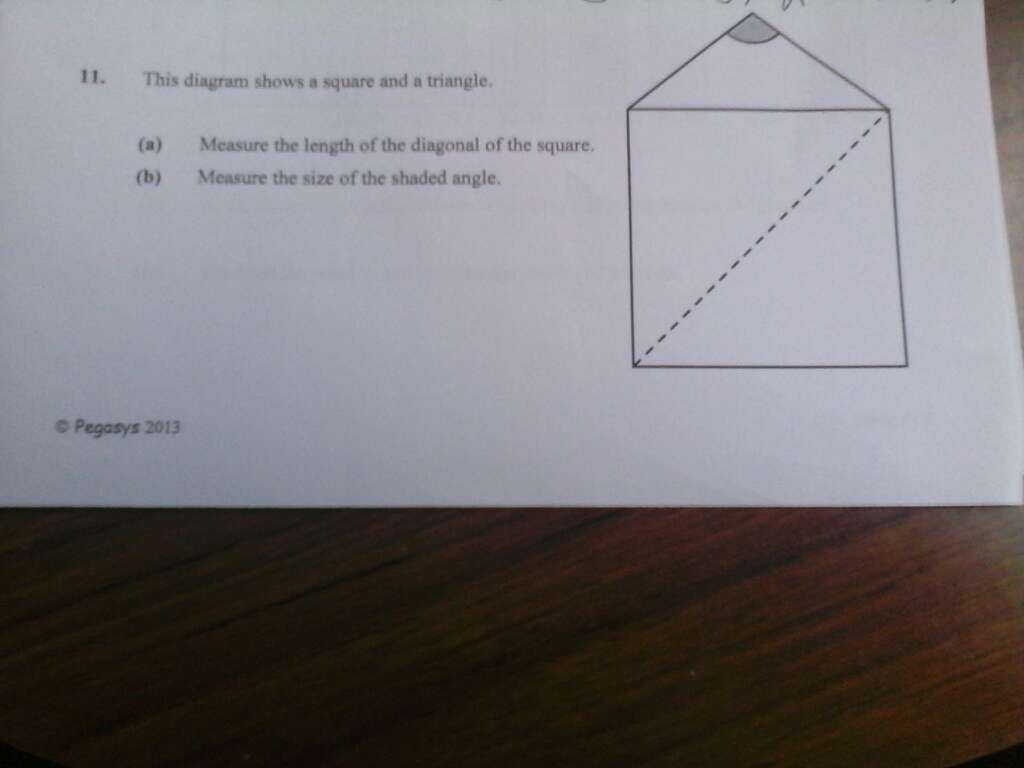
Solution:

You have to do the problem yourself, but I can tell you how exactly you will want to do it.

Step 1: You have to get yourself a ruler and a protractor, if you don't have one already, try to get your mom/dad to buy one for you, or if you are in a hurry, borrow from a classmate.

Step 2: To measure the length of the diagonal, place the ruler on the diagonal. Place to zero mark to the lower left end of the diagonal. Do it exactly as shown.

Step 3: To read the answer, now focus on the part in the diagram above I marked read here. Count the smallest big number of the left hand side and then the number of small fringes. As an example, it may look like this

If you followed all the steps, you should have the answer now, write it down.

Step 4: To measure an angle, you place a protractor you place the middle point of the protractor at the vertex of the angle, and the 0 degree line on the right hand side edge. Do it exactly as shown

Step 5: To read the final answer, now focus on the part of the diagram about I marked as read here again. Count the smallest big number of the left hand side and then the number of small fringes. As an example, it may look like this

Now you should be able to write down the final answer!