Farmer knew Lagrangian optimization!

Problem:



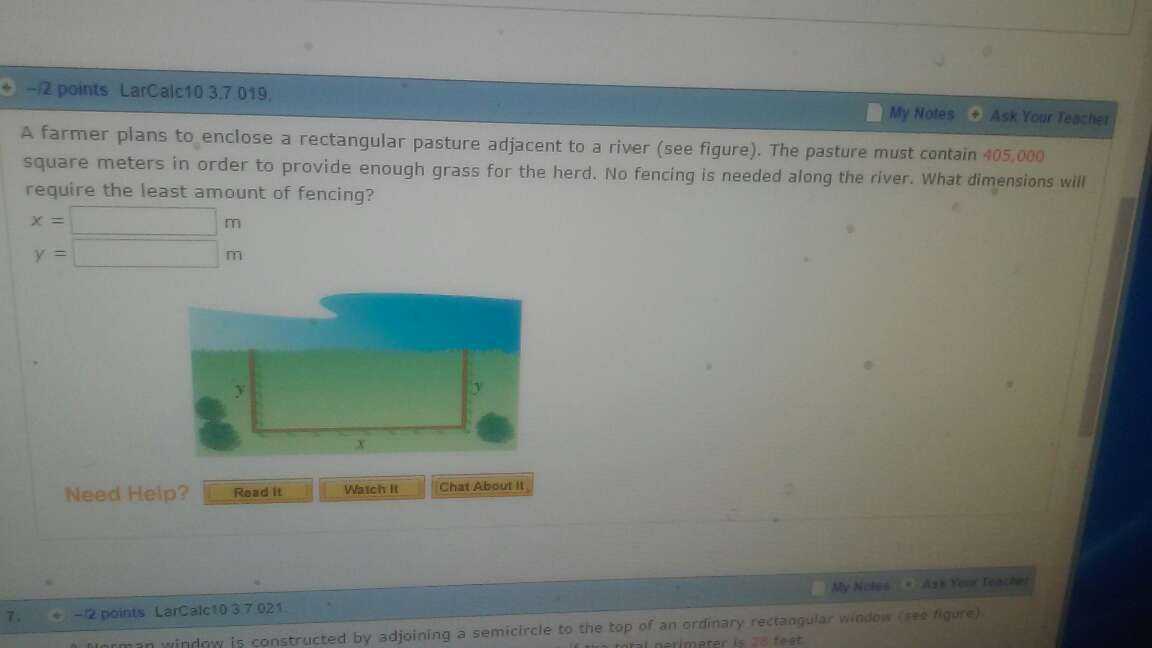
Solution:

Minimize x + 2y subject to xy = 405000

The Lagrangian is

$L(x, y, \lambda) = x + 2y + \lambda(xy - 405000)$

The partial derivatives must be 0, so we get

$1 + \lambda y = 0$
$2 + \lambda x = 0$

Multiply the first equation by $x$ and multiply the second equation by $y$ gives $x - 2y = 0$.

In other words, $x = 2y$, so $xy = 2y^2 = 405000$, $y = 450, x = 900$.