Extra credits

Problem:



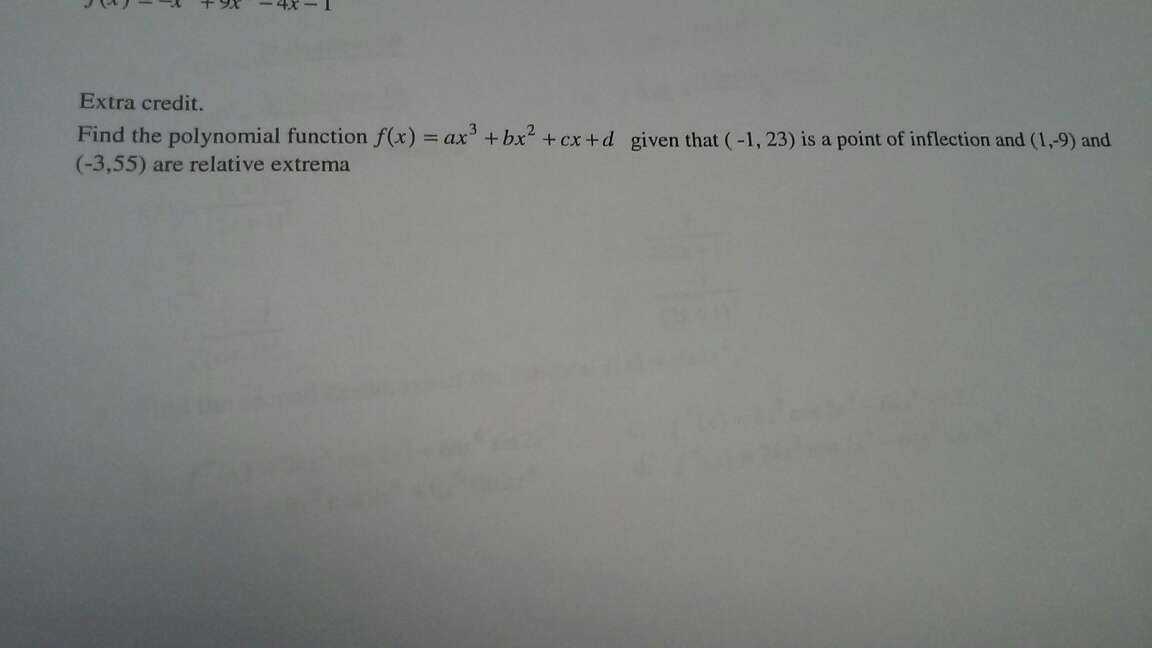
Solution:

$f'(x) = 3ax^2 + 2bx + c$
$f''(x) = 6ax + 2b$

The point of inflection has x coordinate -1, therefore

$6a(-1) + 2b = 0$

The extremas has x coordinate 1 and -3, therefore, 1 and -3 are the roots of  $3ax^2 + 2bx + c = 0$

$3a + 2b + c = 0$
$3a(-3)^2 + 2b(-3) + c = 0$.

The three equations tell us $b = 3a, c = -9a$.

So the equation is $f(x) = ax^3 + 3ax^2 - 9ax + d$

When x = 1, $f(x) = a + 3a - 9a + d = -5a + d = -9$
When x = -1, $f(x) = -a + 3a + 9a + d = 11a + d = 23$

Therefore $a = 2, d = 1$

The final answer is $2x^3 + 6x^2 - 18x + 1$