Verify the identity

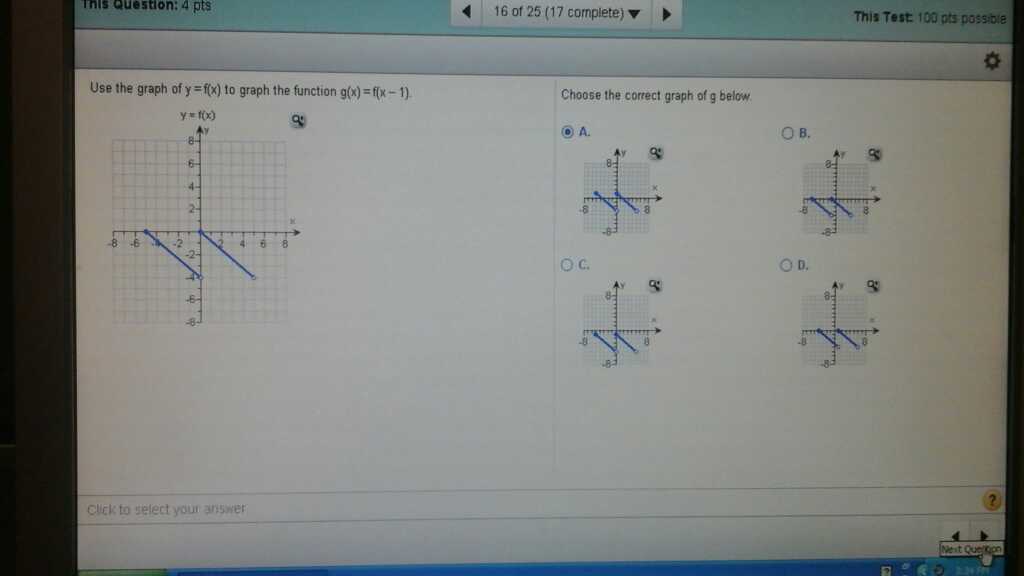
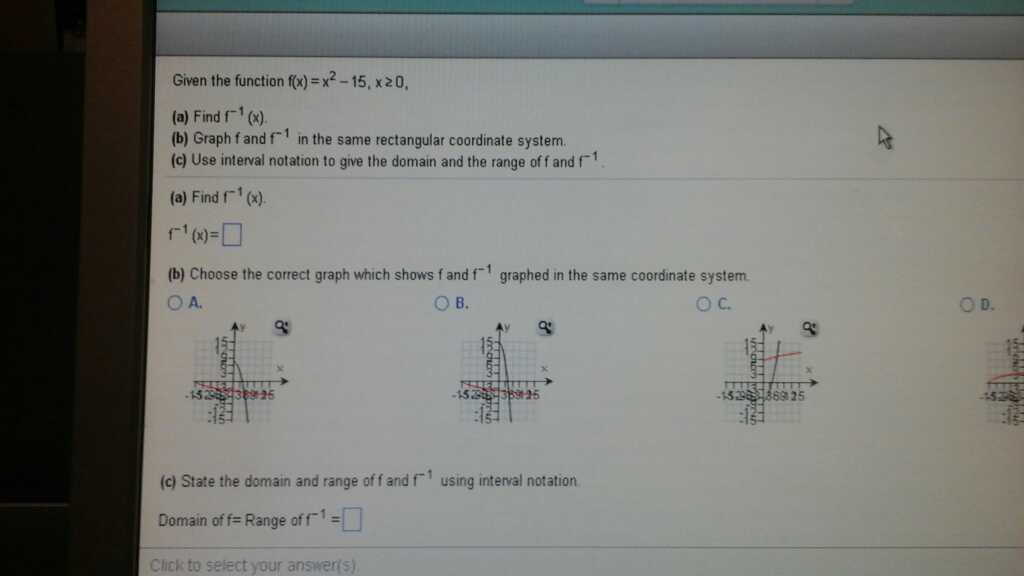
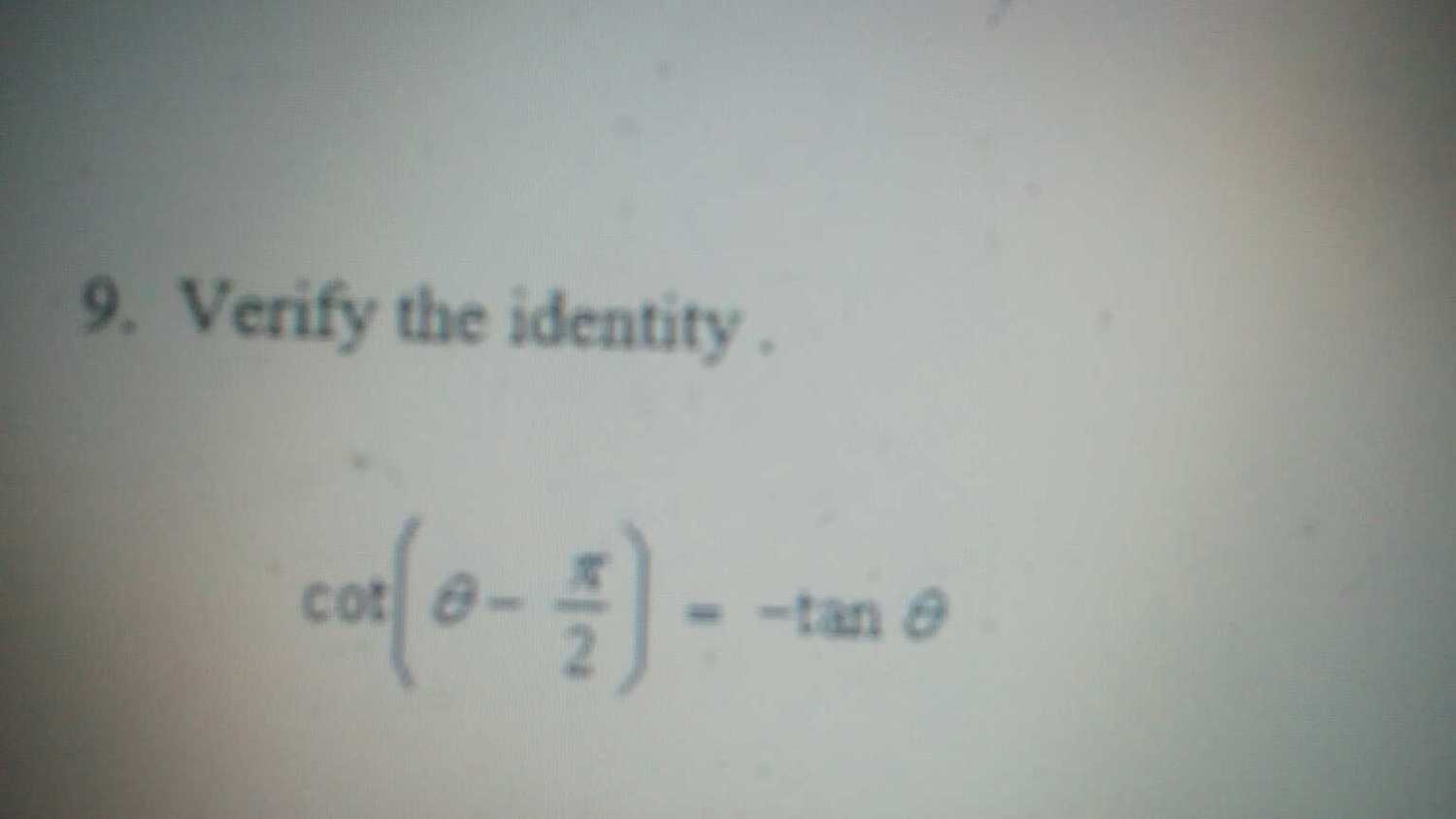Problem:



Solution:

$\cot(\theta - \frac{\pi}{2})$

By definition of cotangent, we have

$= \frac{\cos(\theta - \frac{\pi}{2})}{\sin(\theta - \frac{\pi}{2})}$

By phase shift formulas, we have

$= \frac{\sin(\theta)}{-\cos(\theta)}$

By definition of tangent, we finally get

$= -\tan(\theta)$

Trigonometry problem

Problem:



Solution;

$\frac{\sec \theta}{\csc \theta - \cot \theta} - \frac{\sec \theta}{\csc \theta + \cot \theta}$

Multiply $\sin \theta \cos \theta$ above and below:

$\frac{\sin \theta}{\cos \theta - \cos^2 \theta} - \frac{\sin \theta}{\cos \theta + \cos^2 \theta}$

Make common denominator gives:

$\frac{\sin \theta(\cos \theta + \cos^2 \theta)}{(\cos \theta + \cos^2 \theta)(\cos \theta - \cos^2 \theta)} - \frac{\sin \theta(\cos \theta - \cos^2 \theta)}{(\cos \theta + \cos^2 \theta)(\cos \theta - \cos^2 \theta)}$

Now do the subtraction

$\frac{\sin \theta(\cos \theta + \cos^2 \theta)-\sin \theta(\cos \theta - \cos^2 \theta)}{(\cos \theta + \cos^2 \theta)(\cos \theta - \cos^2 \theta)}$

Simplify the numerator by just expand and subtract:

$\frac{2\sin \theta\cos^2 \theta}{(\cos \theta + \cos^2 \theta)(\cos \theta - \cos^2 \theta)}$

Simplify the denominator:

$\frac{2\sin \theta\cos^2 \theta}{\cos^2 \theta(1 + \cos \theta)(1 - \cos \theta)}$

Cancel the $\cos^2 \theta$:

$\frac{2\sin \theta}{ (1 + \cos \theta)(1 - \cos \theta)}$

Expand the denominator:

$\frac{2\sin \theta}{1  - \cos^2 \theta}$

Just an identity

$\frac{2\sin \theta}{\sin^2 \theta}$

There we go

$2 \csc \theta$

Shift

Problem:



Solution:

We simply check $g(0) = f(-1) = -3$.
So we pick the answer to be D.

Inverse

Problem:



Solution:

Part (a)
$f^{-1}(x) = \sqrt{15 + x}$

Part (b)

Part (c)

The domain of $f$ = Range of $f^{-1}$ = $[0, +\infty)$.
The range of $f$ = domain of $f^{-1}$ = $[-15, +\infty)$.