Differentiate

Problem:



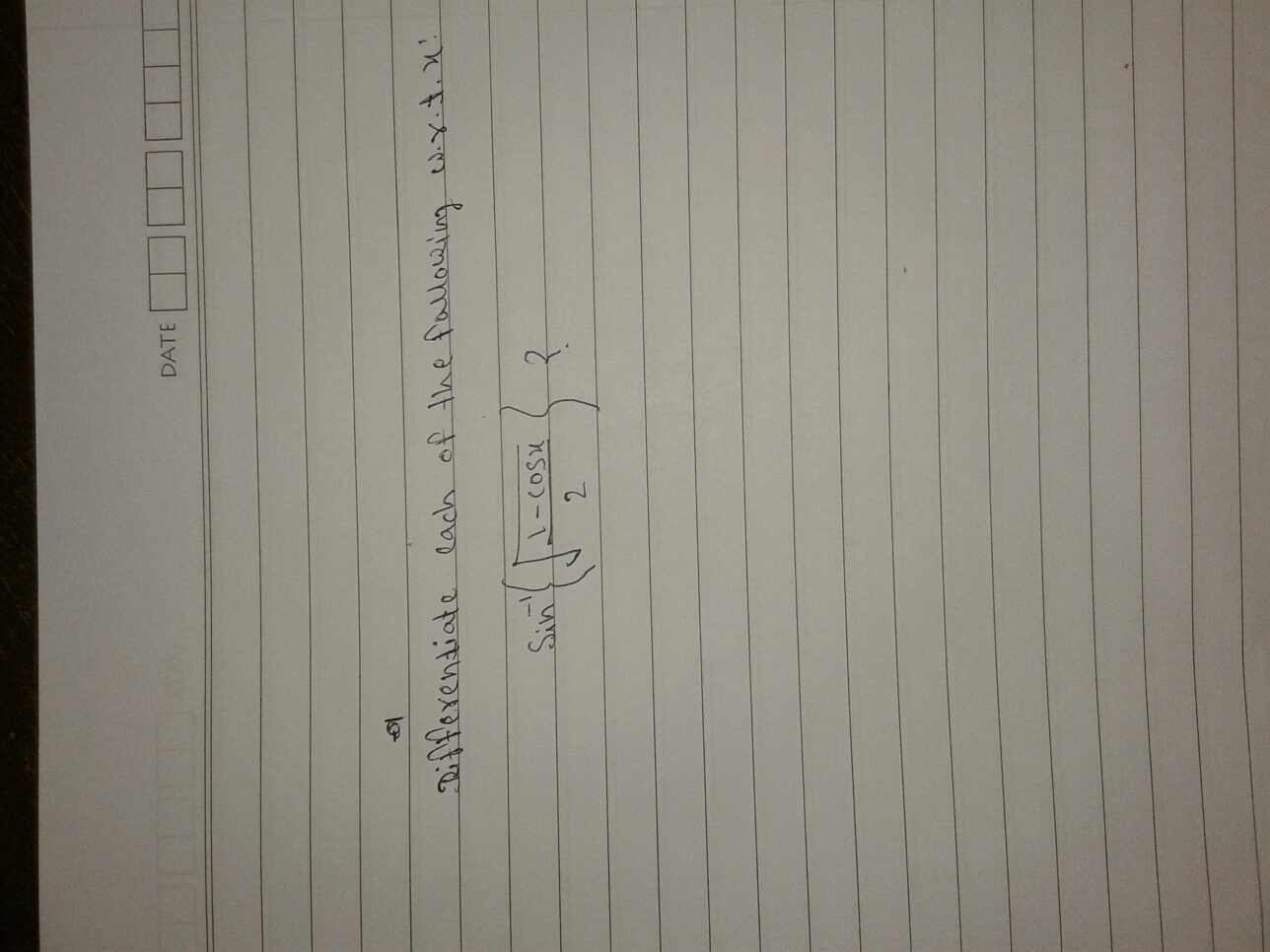
Solution:

Consider $  z = \sin^{-1} y \implies \sin z = y $

$ \cos z\frac{dz}{dy} = 1 $
$ \frac{dz}{dy} = \frac{1}{\cos z} = \frac{1}{\sqrt{1 - \sin^2 z}} = \frac{1}{\sqrt{1 - y^2}} $

The rest is just applying chain rules

$ \frac{d}{dx} \sin^{-1}(\sqrt{\frac{1 - \cos x}{2}}) $
$ = \frac{1}{1 - (\sqrt{\frac{1 - \cos x}{2}})^2} \frac{d}{dx} \sqrt{\frac{1 - \cos x}{2}} $
$ = \frac{1}{1 - \frac{1 - \cos x}{2}} \frac{d}{dx} \sqrt{\frac{1 - \cos x}{2}} $
$ = \frac{2}{2 - (1 - \cos x)} \frac{d}{dx} \sqrt{\frac{1 - \cos x}{2}} $
$ = \frac{2}{1 + \cos x} \frac{d}{dx} \sqrt{\frac{1 - \cos x}{2}} $
$ = \frac{2}{1 + \cos x} \frac{1}{2\sqrt{\frac{1 - \cos x}{2}}} \frac{d}{dx} \frac{1 - \cos x}{2}$
$ = \frac{2}{1 + \cos x} \frac{1}{\sqrt{4\frac{1 - \cos x}{2}}} \frac{d}{dx} \frac{1 - \cos x}{2}$
$ = \frac{2}{1 + \cos x} \frac{1}{\sqrt{2 - 2\cos x}} \frac{d}{dx} \frac{1 - \cos x}{2}$
$ = \frac{2}{1 + \cos x} \frac{1}{\sqrt{2 - 2\cos x}} \frac{\sin x}{2} $
$ = \frac{\sin x}{1 + \cos x} \frac{1}{\sqrt{2 - 2\cos x}}  $