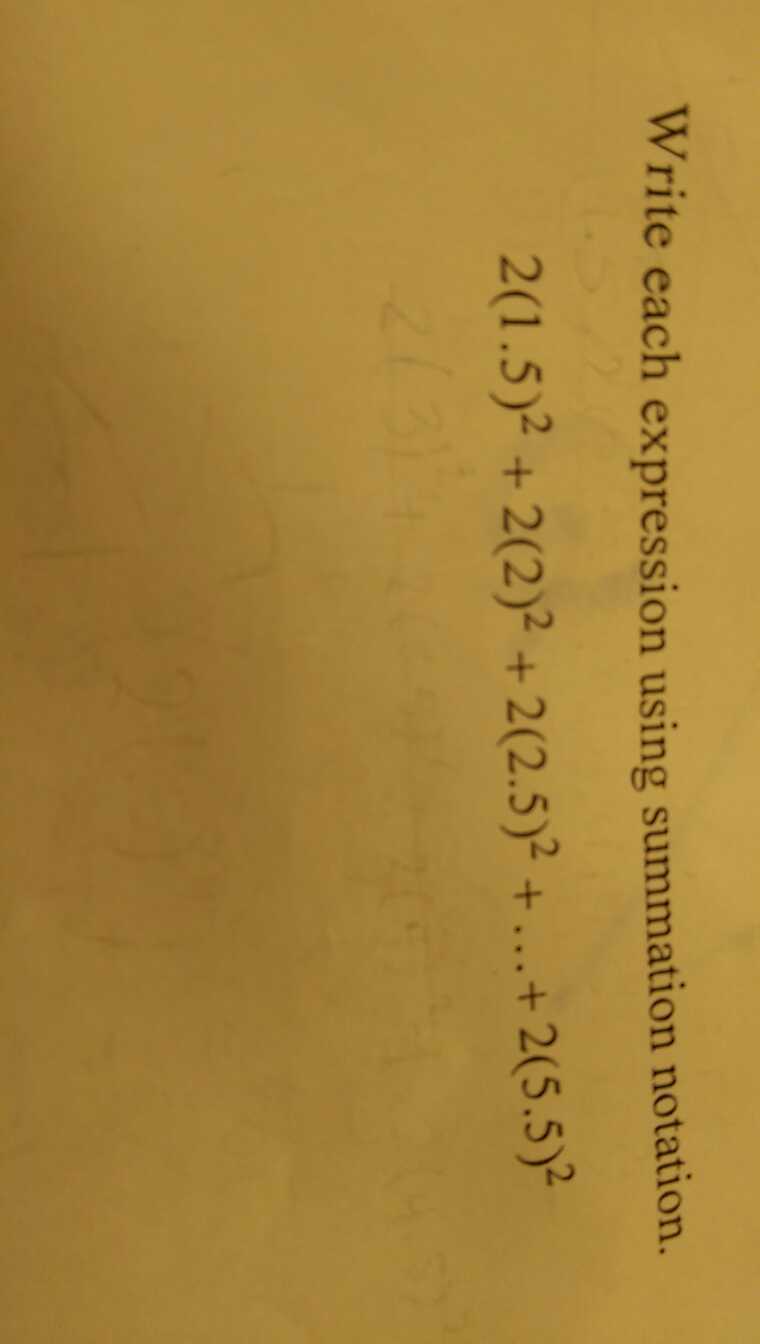Soluability constant

Problem:



Solution:

By the chemical formula, for every cation, we have two anion.

$ [A^-] = 2.2 \times 10^{-4} \times 2 = 4.4 \times 10^{-4} $

Therefore the solubility product $ K_{sp} = [M^{+2}][A^{-1}] = 2.2 \times 10^{-4} \times 4.4 \times 10^{-4} = 9.68 \times 10^{-8} $

Acid dissociation constant

Problem:



Solution:

Let's determine what are the chemicals first.

$ CH_3CO_2H $ is acetic acid, it is a weak acid in aqueous solution.

$ NaCH_3CO_2 $ is sodium acetate, it is a salt.

$ HCl $ is hydrochloric acid, of course.

First of all, we have 100 mL = 0.1 L of the buffer solution, so we have

$ 0.2 \times 0.1 = 0.02 $ mol of $ CH_3CO_2H $ and
$ 0.34 \times 0.1 = 0.034 $ mol of $ NaCH_3CO_2 $.

The salt is an ionic compound, so it dissolves in water and become $ Na^+ $ and $ CH_3CO^-_2 $

The fact that acetic acid is a weak acid means we need to compute how well it dissociate in water using the constant, in particular, we have these two equations

$ pK_a = -\log K_a $
$ K_a = \frac{[A^-][H^+]}{[HA]} $

With the first formula, we can solve for $ K_a = 10^{-4.74} $.

Now we have the reversible reaction:

$ CH_3COOH \to  CH_3COO^- + H^+ $, let say, out of 0.02 mol of $ CH_3COOH $, $ p $ mol of them got dissociated, so we get the total number of moles of elements as:

$ \begin{eqnarray*} [CH_3COOH] &=& 0.02 - p \\ [CH_3COO^-] &=& p + 0.034 \\ [H^+] &=& p \\ [Na^+] &=& 0.034 \end{eqnarray*} $

Plug these values into the $ K_a $ formula, we can solve for $ p $ as follow:

$ 10^{-4.74} = \frac{(p + 0.034)(p)}{0.02-p} $

The resulting quadratic formula has two roots, rejecting the obviously wrong negative solution, we have solved $ p = 1.0695 \times 10^{-5} $.

So the pH value is $ -\log p = 4.97 $.

Now we add hydrochloric acid. We added 8ml = 0.008L of 1M $ HCl $, so we have added $ 0.008 \times 1 = 0.008 $ mol of $ HCl $.

Hydrochloric acid is a strong acid and we assume it completely dissociate (not completely true, but a good approximation), so the number of moles changes as follow:

$ \begin{eqnarray*} [CH_3COOH] &=& 0.02 - p \\ [CH_3COO^-] &=& p + 0.034 \\ [H^+] &=& p + 0.008 \\ [Na^+] &=& 0.034 \\ [Cl^-] &=& 0.008 \\ \end{eqnarray*} $

Now we solve the $ pK_a $ formula again and get $ 10^{-4.74} = \frac{(p + 0.034)(p + 0.008)}{0.02-p} $, but wait, the formula only generate negative $ p $. Now, what does it mean? It means instead of dissociating, the acetate ions take the proton and form the acid instead! In this case, we have $ p = -0.00798 $ and therefore the proton concentration is $ -0.00798 + 0.008 = 1.95684 \times 10^{-5} $, so the pH is $ -\log (p + 0.008) = 4.71 $.

As expected, it becomes more acidic!

How many atoms?

Problem:

Find the number of particles in 15.4g of sodium when one mole has the mass of 23g

Solution:

One mole has mass 23g
15.4g has $\frac{15.4}{23} $ mole
One mole has $ 6.022 \times 10^23 $ atoms.
So we have $ \frac{15.4}{23} \times 6.022 \times 10^23 = 4.032 \times 10^23 $ atoms.

Summation

Problem:



Solution:

$ 2 \sum\limits_{i = 1}^{5}{(i + 0.5)^2} $

Survey design

Problem:



Solution:

a)
The fact that he surveyed people 'entering the dining hall' introducing selection bias.
How about those student just don't bother considering the dining hall? They must have been fed up with the bad food quality!

Pick student with prime student number might work much better, this is more or less simple random sampling.

b)
The fact that the question implies a cost increase introducing bias.
I would worry the price would increase too if I say the food is not good and improved.

That fact that I can only answer yes or not introducing bias.
If I were a student and I think the quality is a little bad but fine, I have no way to express that.

The fact that the manager is asking is introducing response bias.
If I were a student, I would not say the quality of the food is bad to dismay the boss (I would worry if he will serve me bad food moving forward)

The fact that there is 1 common dining hall is introducing bias.
Without comparison it can be hard to tell food quality.

It can be done through an anonymous survey, the question should look like this:

In rating 1 - 10, what do you think is the quality of the food in the dining hall?
In rating 1 - 10, what do you think is the quality of the food in the Mcdonald?
In rating 1 - 10, what do you think is the quality of the food in the XXX (Some other competitor) ?

A few design points here:

• By staying anonymous, student can feel free responding without worry retaliation.
• By comparing, researcher can make sense out of the relative scale.
• By having many rating, student can now choose, something like 3 - 7 to indicating slightly like/dislike instead of just yes or no.

Sampling

Problem:

Solution:

5)

(a) Selection bias means the samples are not properly selected, leading to systematic bias. For example, using mother goes pickup their children after school, if we select people by picking parent who go to pick up kids, we might turn out bias towards woman's view.

(b) Response bias means the answer are impacted not just by the question alone, but by other factors. For example, a black person is conducting a survey, and one question ask your opinion about black people, you are most likely to give answer that favor black people anyway despite what you think.   

(c) Non response bias is simply the participant refuse to answer the question. In most cases, the people who do not response actually have strong opinion and expressing that as not responding, that can lead to bias too. Voting is a great case for this. If we do not want to researcher to know who will we vote, we will refuse to response to the survey and do the voting to surprise the researcher.   

6)

Question bias towards keeping.

Do you think U.S. should responsibly keep the troops at Iraq?

The question implies leaving as not responsible, so a sensible responder would say yes.

Question bias towards leaving.

Do you think U.S. should be done with keep the troops at Iraq?

The question implies U.S. has stay there for long and should be done with it.

Differentiate

Problem:



Solution:

Consider $  z = \sin^{-1} y \implies \sin z = y $

$ \cos z\frac{dz}{dy} = 1 $
$ \frac{dz}{dy} = \frac{1}{\cos z} = \frac{1}{\sqrt{1 - \sin^2 z}} = \frac{1}{\sqrt{1 - y^2}} $

The rest is just applying chain rules

$ \frac{d}{dx} \sin^{-1}(\sqrt{\frac{1 - \cos x}{2}}) $
$ = \frac{1}{1 - (\sqrt{\frac{1 - \cos x}{2}})^2} \frac{d}{dx} \sqrt{\frac{1 - \cos x}{2}} $
$ = \frac{1}{1 - \frac{1 - \cos x}{2}} \frac{d}{dx} \sqrt{\frac{1 - \cos x}{2}} $
$ = \frac{2}{2 - (1 - \cos x)} \frac{d}{dx} \sqrt{\frac{1 - \cos x}{2}} $
$ = \frac{2}{1 + \cos x} \frac{d}{dx} \sqrt{\frac{1 - \cos x}{2}} $
$ = \frac{2}{1 + \cos x} \frac{1}{2\sqrt{\frac{1 - \cos x}{2}}} \frac{d}{dx} \frac{1 - \cos x}{2}$
$ = \frac{2}{1 + \cos x} \frac{1}{\sqrt{4\frac{1 - \cos x}{2}}} \frac{d}{dx} \frac{1 - \cos x}{2}$
$ = \frac{2}{1 + \cos x} \frac{1}{\sqrt{2 - 2\cos x}} \frac{d}{dx} \frac{1 - \cos x}{2}$
$ = \frac{2}{1 + \cos x} \frac{1}{\sqrt{2 - 2\cos x}} \frac{\sin x}{2} $
$ = \frac{\sin x}{1 + \cos x} \frac{1}{\sqrt{2 - 2\cos x}}  $